As diaphragm is considered a structural element that can transmit lateral loads to the vertical resisting elements of a structure, i.e. columns and shear walls. The term diaphragm is usually applied to roofs and floors. However, a shear wall is a vertical, cantilevered diaphragm. These construction systems can be used when designing a building for seismic or wind lateral loads.
The diaphragm forces are transferred to the vertical resisting elements primarily through in-plane shear stress. The most common lateral loads to be resisted are those resulting from earthquake and/or wind actions. Secondarily, other lateral loads, i.e. earth or hydrostatic pressure, can be also resisted by diaphragm actions.
Furthermore, the diaphragm of a structure supports gravity loads, especially in bridges. Diaphragms are usually constructed of concrete slab referring to concrete structures or metal or composite metal deck in steel structures.
The three primary types of diaphragm are flexible, rigid and semirigid. Flexible diaphragms resist lateral forces depending on the tributary area, irrespective of the flexibility of the members that they are transferring force to. On the other hand, rigid diaphragms transfer load to frames or shear walls depending on their flexibility and their location in the structure. The flexibility of a diaphragm affects the distribution of lateral forces to the vertical components of the lateral force resisting elements in a structure. The main difference of rigid diaphragms and semirigid diaphragms is that a rigid diaphragm has infinite in-plane stiffness properties, and therefore it neither exhibits membrane deformation nor report the associated forces, whereas a semi-rigid diaphragm simulates actual in-plane stiffness properties and behavior.
What is of interest of a (structural) civil engineer is mainly the modeling and the classification of the diaphragms. Diaphragms are a part of an analytical model in most cases and thus the knowledge of the theory is significant for an ordinary user of a software. The main function of diaphragms is to provide stability to the overall structure when the structure is subjected to lateral loads and a careful handling of the model is appropriate.
The current text is written in continuation of the following posts:
It summarizes the history and the types of diaphragms, the characteristics and modeling of flexible diaphragms, the classification and special considerations for rigid diaphragms, the characteristics and modeling of semirigid diaphragms and the impact of mesh size in semirigid diaphragm analysis.
Over the last several years we have seen a steady evolution in how diaphragms are considered in analysis programs.
Prior to the mid-1980s, before structural analysis software was readily available to engineers, most engineers analyzed buildings for lateral loads using simplified manual methods, considering the frames as individual 2D frames. Loads were considered as nodal loads, which had to be calculated by hand (the codes were much simpler back then) and the engineer had to decided how to distribute the loads to each frame. This was generally based either on tributary areas or on relative stiffnesses of the frames. It is interesting to note that implicit in the former approach was the assumption of a flexible diaphragm and implicit in the methodologies commonly used in the latter approach was the assumption of a rigid diaphragm.

With the advent of personal computers, rudimentary analysis programs became generally available, but those programs merely mimicked what engineers were previously doing manually: engineers analyzed most buildings for lateral loads by simply modeling separately each individual 2D frame and applying the nodal loads that the engineer manual calculated. There were no capabilities to analyze the 3D frames nor to automatically generate wind or seismic loads in those programs.
By the late 1990s, however, the technology evolved. Three-dimensional models could now be created and analyzed within a software program, and lateral loads could now be automatically generated and distributed to the lateral frames in the model. Nodal loads could still be manually calculated and meticulously applied if desired, but the software could also automate the process of applying the wind and seismic story forces and distributing those loads to the various frames. Because of severe limitations on computer memory and speed, simplifying assumptions and methodologies were necessary. The assumption that the diaphragm is infinitely rigid was widely implemented because it dramatically reduced the size of the analytical model while providing a mechanism for distributing the wind and seismic loads to the frames. At the time it was impractical or impossible to actually model the diaphragm properties and include the diaphragm as part of the analytical model.
Today’s computers are exponentially faster and have much more capacity for larger and more complicated analytical models. This includes the ability to explicitly model the diaphragms and include them in the analysis. But it is still common today for engineers to consider diaphragms to be either flexible (i.e., no significant stiffness) or to be rigid, and to analyze them that way without any modeling of the diaphragms.
Why is it important to know this history? First, it is important to understand how and why commonly accepted practices and method originated. It helps justify using a particular approach, or demands that something different be done. While engineers now rely heavily on automated technology, it is sometimes necessary to do hand calculations to verify results; knowledge of this history can help with that manual process.
Second, it helps answer confusion about the methods used and the results obtained, and clarifies best practices and methods for particular conditions. This understanding aids in determining the ramifications of employing any particular diaphragm modeling methodology, and guides the engineer in mitigating the shortcomings inherent with each.
When the lateral stiffness of the frames is very large compared to the in-plane stiffness of the diaphragm, the diaphragm has very little influence on the distribution of lateral forces. Such a diaphragm is classified as Flexible. It lacks the capacity to redistribute forces between frames. In the extreme, horizontal braces are sometimes required to provide the load paths to the frames. Often with the help of drags and chords it is capable of distributing the lateral loads to the frames simply based on tributary exposure (for wind) or tributary area (for seismic). This is common for metal roof decks. These diaphragms are not represented in the analytical model in any way; the lateral model consists only of the frame members. There is no mechanism analytically to transfer the lateral forces to the frames, and so the loads must be explicitly assigned as nodal loads by the engineer. This modeling is closest to the way that analysis was done before 3D programs became available.

In contrast to the Flexible diaphragm, some diaphragms are very stiff compared to the stiffness of the frames; the in-plane deformation of the diaphragm is very small compared to the horizontal deflections of the frames. Due to the lack of capacity and capabilities in early computers it became common to simplify the analytical model by assuming that the diaphragm is infinitely rigid. This is what is known as the Rigid diaphragm. The size of the computational model is reduced drastically when this assumption is made (which was necessary when computers had much less processing power). The Rigid diaphragm can rotate and translate, but it cannot deform. In such a model, the lateral forces will be distributed (and redistributed at subsequent levels) based upon the relative stiffnesses of all the members resisting lateral loads. Because concrete floors and floors of concrete fill on metal deck are generally very stiff, the Rigid diaphragm is often a suitable representation. It provides a convenient analytical tool for tying the frames together and distributing the story forces to the various frames. It is interesting to note that hand methods that were used, before computers were readily available, to attempt to distribute the loads to the frames based on the relative stiffnesses of the frames were based on an implicit assumption that the diaphragms were Rigid.
Many diaphragms don’t qualify as either Flexible or Rigid. The in-plane deformations of the diaphragm have significant influence on the distribution of lateral forces to the frames. Such diaphragms are referred to as Semirigid. To adequately capture these effects the diaphragm must be modeled and included explicitly in the analysis. This requires that the diaphragm stiffness properties be specified and the diaphragm meshed into shell or plate elements. This dramatically increases the size of the analytical model and the time that it takes to analyze. Historically this was not feasible due to the limited memory and capacity of computers, but that is no longer the case. The Rigid diaphragm assumption is still useful and can be adequately valid in many cases, but an over-reliance on the use of the Rigid diaphragm assumption has led to more and more stringent requirements in Building Codes specifying when the diaphragms must be modeled as Semirigid.

ASCE 7-16 Section 12.3.1.1 describes configurations in which the diaphragm may be considered Flexible, generally including untopped steel decking or wood structural panels in structures where the lateral force resisting system is braced frames or shear walls. Refer to that section for other configurations as well. Note that it doesn’t say that such diaphragms must be considered Flexible, it only says that it is permitted to consider such diaphragms as Flexible. Also note that this is in the chapter on seismic design requirements; in Chapter 26 for wind loads, Section 26.2 gives a much simpler definition for “Diaphragm” that permits more configurations to be considered Rigid. For simplicity, however, I recommend that when designing for both seismic and wind loads, the same diaphragm definition and modeling be used for both, and that will generally be based on the more stringent diaphragm definition given for seismic design.
When the structural conditions do not fall within the category described in ASCE 7-16 Section 12.3.1.1, it is still permitted to consider the diaphragm as Flexible if the deflection of the diaphragm is greater than two times the drift of the adjacent frames as described in Section 12.3.1.3. A difficulty with this provision, however, is that the deflection of the diaphragm must be determined, either analytically or manually.

As can be seen, ASCE 7 has very explicit definitions of diaphragm types. In jurisdictions where other Codes are used, the requirements of those codes related to diaphragms should be investigated. Some codes merely have a general but ambiguous statement to the effect that the analysis shall consider “the influences that may reasonably be expected”, one of many of which is the diaphragms. In the Eurocodes I have only found references to diaphragms in Eurocode 8: Design of structures for earthquake resistance. Most of those references are descriptions of Rigid diaphragms, with no explicit reference to Flexible diaphragms. In lieu of explicit definitions in those codes, the definitions given in ASCE 7 are reasonable.

It is common that the Roof diaphragm is classified as Flexible and the floor diaphragms are classified as Rigid or Semirigid, and it is acceptable to analyze them as such. In analysis software, when considering a diaphragm as Flexible, the beams, columns, braces and walls are modeled but no element is modeled to represent the diaphragm. This simplifies the modeling of the structure but complicates the application of the loads. For Rigid and Semirigid, the diaphragm provides the analytical method for distributing the lateral forces to the frames, but since there is nothing in the model that represents the Flexible diaphragm, determination of the distribution of the lateral forces to the frames must be done manually. For seismic forces this is often based on a tributary area basis and for wind forces on a tributary exposure basis. Essentially, the loads will take the shortest path through the diaphragm to the nearest frame members.
It is crucial that the capacity of the decking and framing be investigated to verify that it is capable of transferring those forces, otherwise serious damage and even collapse may occur. If necessary, members and connections should be designed as drags to convey the lateral forces through the decking to the frames.
Because there are no diaphragm elements in the model to provide lateral bracing to the frame members, care must be taken to avoid creating conditions that are analytically unstable. This can occur, for example, if all of the columns in a frame are pinned in the weak axis; there is nothing to resist those columns from “tipping over” sideways.
An off-topic but important consideration is the ability or lack thereof of the deck to brace the top flange of the beam. If it is so flexible that it is considered a Flexible diaphragm, it may lack the stiffness required to be considered a brace of the top compression flange, in which case the beam should be designed considering the full unbraced length.
Some diaphragms, such as concrete slabs, are very stiff compared to the stiffness of the frames; the in-plane deformation of the diaphragm is negligible compared to the horizontal deflections of the frames. Such diaphragms can be classified as Rigid. Analytically, Rigid diaphragms are considered to be infinitely rigid. The Rigid diaphragm can rotate and translate, but it cannot deform. In such a model, the lateral forces will be distributed (and redistributed at subsequent levels) based upon the relative stiffnesses and location of all the members resisting lateral loads. It provides a convenient analytical tool for tying the frames together and distributing the story forces to the various frames.

ASCE 7-16 Section 12.2.1.2 gives a very narrow definition of when a diaphragm can be considered Rigid:
Diaphragms of concrete slabs or concrete-filled metal deck with span-to-depth ratios of 3 or less in structures that have no horizontal irregularities are permitted to be idealized as rigid.
Concrete slabs and composite slabs are recognized as being very stiff. The span-to-depth ratio does not refer to that of the slab itself, but rather the ratio of the distance between frames (“span”) to the width of the diaphragm (“depth”). If the diaphragm is long and narrow, it can’t be considered a Rigid diaphragm.

Horizontal Irregularities are defined in Table 12.3-1 of ASCE 7-16. I could fill a whole article just discussing these (maybe I will).
The IBC gives a more liberal definition of Rigid diaphragm. In Section 1604.4 of IBC 2018 it states:
A diaphragm is rigid for the purpose of distribution of story shear and torsional moment when the lateral deformation of the diaphragm is less than or equal to two times the average story drift.
Note that this is similar but opposite of the ASCE 7 definition of Flexible. And again, it requires that the deflection of the diaphragm be determined, either analytically or manually, in order to determine whether or not the diaphragm can be modeled as Rigid.
The Eurocode allows a diaphragm to be modeled as Rigid if the corresponding Semirigid model doesn’t produce horizontal displacements that exceed the Rigid diaphragm’s model by more than 10%. The Note to Clause 4.3.1(4) of EN 1998-1:2004+A1:2013 states:
NOTE The diaphragm is taken as being rigid, if, when it is modelled with its actual in-plane flexibility, its horizontal displacements nowhere exceed those resulting from the rigid diaphragm assumption by more than 10% of the corresponding absolute horizontal displacements in the seismic design situation.
In some analytical programs, the Rigid diaphragm is modeled by the user defining a master node and then constraining to that node all of the other nodes at that level. In the RAM Structural System and some other programs the diaphragm is simply specified by the user as Rigid and then during the analysis process when the stiffness matrix is formed, none of the degrees of freedom associated with the diaphragm are included. This drastically reduces the size of the matrix, able to be analyzed significantly faster and with far fewer computing resources. This is one reason the assumption has been so popular since the early days of computing.
In this chapter the discussion is continued for Rigid diaphragms, highlighting some issues of concern that need to be understood and considered.
Consider a beam in a moment frame or braced frame. Because analytically the Rigid diaphragm is modeled as infinitely rigid, any two points on the diaphragm can translate and rotate, but the distance between them remains fixed. If both ends of a frame beam are attached to the Rigid diaphragm, the distance between them remains fixed; that is, there is no shortening or elongation of the beam – there is no axial strain in the beam. Since stress is a function of strain (stress = E times strain), if there is no strain there is no stress – which means no axial force. Of course this is wrong, in reality there will be axial force in the beams, but because of the Rigid diaphragm the analysis indicates zero axial force. This concept is important to understand because automated designs of these members won’t include an axial load component. This may not be significant for a moment frame beam that generally is only distributing the lateral forces to the columns; in compression the concrete floor slab may take a significant portion of that axial force, and in tension the beam may have sufficient additional capacity for the relatively small axial force. However, this can be a significant error for braced frame beams, especially for brace configurations in which the beam is a significant part of the load path in distributing the cumulative lateral force from the braces above to the braces below; these beams carry significant axial load but the analysis does not indicate that. This shortcoming of the Rigid diaphragm assumption can be rectified by selectively disconnecting some nodes from the diaphragm. For example, at each level consider disconnecting all but one of the nodes in each frame. Take care not to disconnect too many nodes, otherwise the forces will not get from the diaphragm to the frames. For chevron braces the node where the brace connects to the midspan of the beam should be disconnected from the diaphragm; the RAM Structural System automatically does this.

This figure shows the nodes, with the yellow nodes indicating those that are attached to the diaphragm and the white nodes indicating those that have been detached from the diaphragm. When analyzed, the forces in the diaphragms will be transferred into the frames at the yellow nodes and distributed to the adjacent nodes via axial forces in the beams, as expected:
Note that this approach will likely be conservative because it may overstate the axial load in the beams, since in reality the diaphragm forces are transferred into the frame at all of these node points, not just one and then distributed through the beams.
Obviously, nodes that are outside of the floor slab should not be connected to the Rigid diaphragm. The RAM Structural System provides tools that allow slab edges and openings to be quickly and easily modeled, and the determination of whether or not a member’s nodes are within that diaphragm – and hence attached to the Rigid diaphragm – is fully automated. With this and any other programs with similar capabilities it is important to recognize the potential that nodes intended to be (or should be) outside of the Rigid diaphragm are included in the Rigid diaphragm, and are not disconnected as they should be. Consider two different ways of modeling the slab shown in the following figure:

In the figure on the left, the slab edge is assigned to the perimeter framing, with an opening assigned in the interior. In the figure on the right, the slab edge cuts into the interior of the framing, leaving some framing exposed. The figure on the right is most likely the way it will actually be constructed. In the figure on the right the column at A-1 will be correctly disconnected from the diaphragm; lateral forces in the diaphragm can only be distributed to that column through axial force in the beam, not directly from the diaphragm to the column. However, in the figure on the left the column at A-1 is within the area bounded by the diaphragm edge, and so would automatically be connected to the Rigid diaphragm. In the analysis that column would be perceived to be capable of receiving lateral forces directly from the diaphragm. Remember, in a model where the diaphragm is considered to be infinitely rigid, openings in the diaphragm have no impact on the analysis results. This could have a large impact on the axial force reported by the analysis, and would certainly impact the flow of forces in the braces in braced frames. Of course, this problem could be dealt with by selectively disconnecting the node from the diaphragm, as was discussed above.
Finally, it is important to recognize that when a diaphragm has been specified as Rigid, the slab openings and even the geometry of the diaphragm itself has no influence on the analysis results. Consider this model, for example:

You would expect the opening and the narrow diaphragm to have a significant impact on the behavior of this structure. However, if this diaphragm has been specified as Rigid the opening and narrow width are ignored; the diaphragm doesn’t deform, the distribution of the horizontal diaphragm forces is based solely on the relative stiffnesses of the frames and their location. This could result in significant error in the distribution of lateral forces to the various frames, resulting in some frames being underdesigned and incapable of resisting the forces that they are likely to receive. This is the very reason why the building codes restrict the use of the Rigid diaphragm assumption; it is inappropriate for structures such as these.
Many diaphragms require more than simply being considered completely flexible or infinitely rigid. Often the actual stiffness of the diaphragm itself plays a key role in the distribution of the lateral forces to the various frames.
Classifying Semirigid Diaphragms
Classifying Flexible Diaphragms
Unless a diaphragm can be idealized as either flexible or rigid in accordance with 12.3.1.1, 12.3.1.2, or 12.3.1.3, the structural analysis shall explicitly include consideration of the stiffness of the diaphragm (i.e., semi-rigid modeling assumption).
ASCE 7-16 Section 12.3.1.1 permits a diaphragm to be considered Flexible when the diaphragm consists of untopped steel decking or wood structural panels in structures where the lateral force resisting system is steel or composite steel braced frames, or concrete, masonry, steel or composite steel shear wall. These are explicitly identified because they are very stiff relative to an untopped steel deck or wood panel floor system. Diaphragms in one- and two-family dwellings, and shttps://blog.virtuosity.com/special-considerations-for-rigid-diaphragmstructures of light-frame construction – with some restrictions – are also permitted to be considered Flexible.
Section 12.3.1.3 further permits any diaphragm to be considered Flexible if the deflection of the diaphragm is greater than two times the drift of the adjacent frames.
Classifying Rigid Diaphragms
Conversely, in Section 12.3.1.2 the only diaphragm condition that is permitted to be considered Rigid is diaphragms of concrete slabs or concrete-filled metal deck with diaphragm span-to-depth ratios of 3 or less in structures that have no horizontal irregularities.
All other diaphragms, according to Section 12.3.1, are required to be considered as Semirigid. This represents a significant portion of structures.
It is interesting to note that IBC 2018 categorizes diaphragms differently. Because IBC 2018 references ASCE 7-16 with no changes to the definition of Flexible diaphragm, the requirement of Section 12.3.1.3 of ASCE 7-16 applies, in which a diaphragm can be considered to be Flexible if the lateral deflection of the diaphragm is greater than two times the drift of the adjacent frames. But then in Section 1604.4 of IBC 2018 the definition of Rigid diaphragm is modified from that found in ASCE 7:
A diaphragm is rigid … when the lateral deformation of the diaphragm is less than or equal to two times the average story drift.
Characteristics of Semirigid Diaphragm
Hence, per the IBC, all diaphragms can be considered as either Flexible or Rigid. Simply put, categorize the diaphragm by comparing diaphragm deflection to frame deflections: if that ratio is more than two, the diaphragm can be analyzed as flexible; if that ratio is less than or equal to two, the diaphragm can be analyzed as rigid. I don’t recommend this, however; I believe that the ASCE 7 definition is generally more appropriate. It may also be more practical to analyze the diaphragms as semirigid since such an analysis would be required anyway to perform the deflection calculations necessary to classify the diaphragms as one or the other. It is permissible in any case to model and analyze the diaphragm as semirigid.
As I indicated above, Section 12.3.1.2 of ASCE 7 does not allow diaphragms of structures with horizontal irregularities to be analyzed as Rigid. This is due to the fact that diaphragms in such structures may play a larger role in the behavior of the structure and in the distribution of the forces to the lateral force resisting system. The diaphragms may play a larger role in mitigating the potential damage to the structure due to the irregularities. In such cases it is important to know the forces in and displacements of the diaphragm so that it can be properly designed. Furthermore, structural irregularities are often localized conditions, so it is important that the local impacts of the diaphragm flexibility are considered in the analysis. For example, unless there is a horizontal floor truss, when there is a Horizontal Offset Irregularity the diaphragm is the mechanism for distributing the lateral forces out of the frame above over to the frame below. A torsional irregularity is evidence of a poor distribution of frames and frame stiffness, or of a highly uneven distribution of diaphragm masses; this is likely to place more demand on the diaphragm, and requires a more accurate consideration of how the diaphragm is interacting with the frames. Similarly, frames in nonparallel systems have a much higher degree of interaction than orthogonal frames, and are tied together to the degree that the diaphragm is capable.
In a building with multiple wings the floor may consist of a very stiff concrete slab; despite that, a rigid diaphragm analysis would probably not be appropriate. In a rigid diaphragm analysis, the far ends of the wings would be constrained to translate and rotate together. A semirigid diaphragm analysis would more correctly allow those wings to displace independently of each other, tied together only by the stiffness of the diaphragm where the wings meet at the core.

A diaphragm with large openings would obviously not behave the same as a solid diaphragm.
And a long, narrow diaphragm could be rigid in one direction but not in the other.
Although historically the influence of diaphragms was given lesser consideration, and simplified approximated methods were allowed due to the need to use more simple hand and analytical techniques, increasingly the structures designed and built today need more robust analysis. Incorporation of semirigid diaphragms in the analysis is part of that.
Creation, analysis, and review of a model with Semirigid diaphragms requires considerably more effort by the engineer and more computing resources in the computer. If done properly it also gives the most realistic and correct design results. The first step is to define the analytical properties of the slab or deck:
For a concrete slab it is common to use the slab thickness and the concrete properties (e.g., Ec) to define the diaphragm stiffness; it may be appropriate to apply a cracked factor to Ec.
For concrete fill on metal deck it is common to ignore the contribution of the metal deck, and only use the concrete properties to define the diaphragm stiffness. Although some engineers consider the diaphragm to be only the depth of the concrete above the ribs, it would be appropriate to consider all of the concrete, including that in the ribs, since the concrete in the ribs contributes to the shear stiffness of the diaphragm in both directions; for most open-profile/trapezoidal decks this is most easily done by specifying a diaphragm thickness equal to the depth of fill plus one-half of the rib depth. For reentrant profile decks an equivalent depth can be calculated and used. Although unusual, some engineers apply a cracked factor to these diaphragms as well (in defense of the practice of ignoring a cracked factor for these decks I would suggest that the metal deck, acting compositely with the concrete, adds considerable stiffness, which we are ignoring, to make up for ignoring the cracked factor).
The stiffness of other types of decks is more difficult to define. For example, the stiffness of metal roof deck is dependent on the gauge of the deck, the attachment of the deck to the beams and to adjacent deck sheets, the beam spacing, and the susceptibility of the corrugated ribs to warping, among others. The Steel Deck Institute manual provides some guidance. Some engineers insist that different stiffness values should be used parallel to the span versus perpendicular to the span of the ribs. However, Section 3.1 of the Steel Deck Institute’s Diaphragm Design Manual 3rd Ed. shows the calculation of the stiffness, G’, without regard to the direction of the deck span, noting that “the average shear … is equal either along the panel direction or across the panels.” So, keep it simple.
The stiffness of plywood diaphragms is similarly difficult to define.
Defining Extents of the Diaphragm
The next step is to define the extents of the diaphragm. This is generally the extents of the slab edge around the perimeter of the structure. All significant openings in the slab must also be modeled; if relatively large, these can significantly reduce the stiffness of the diaphragm. The connectivity of the frame columns, beams, and walls to the diaphragm must then be specified; these members must share a common node with the diaphragm. In the RAM Structural System this is done automatically; all frame members within the slab edge boundaries are automatically connected to the diaphragm.
With the diaphragm stiffness properties defined and the diaphragm boundaries identified, the next step is to mesh the diaphragm into discrete plate or shell elements. Some programs, such as the RAM Structural System, automatically create the diaphragm mesh as seen here:

With the addition of all of these mesh elements the analysis will take considerably longer than for the model with rigid diaphragms. Furthermore, the coarseness of the mesh (the size of the plate elements) is a consideration in both the accuracy of the results and the time required for the analysis, with a generally small impact on the former and a large impact on the latter.
The final step is to define the loads on the diaphragm. Because the semirigid diaphragm is less stiff than a rigid diaphragm, the analysis is likely to indicate a longer fundamental building period for the model with the semirigid diaphragm than the rigid diaphragm; the longer period may result in a smaller base shear for seismic loads. This is appropriate. The rigid diaphragm analysis may give shorter building periods and, hence, larger base shears, which are conservative. In most cases, however, the difference is expected to be minor.
Diaphragm displacements and story drifts given by the semirigid diaphragm analysis will differ somewhat from a rigid diaphragm analysis due to the locally greater (or smaller) deflections that result from not being constrained by the rigid diaphragm assumption. In regions of the diaphragm not immediately adjacent to the lateral frame members, these differences may be particularly greater; the validity of those values reported by the semirigid analysis should be questioned because although the properties of the slab or deck are more accurately defined, the diaphragm displacements at locations away from the lateral frames may be exaggerated without consideration of the constraining effects of the gravity framing, which normally isn’t included in the lateral analysis for simplicity.
It is difficult to perform independent verification calculations other than some simplified approximations. Furthermore, the output is more complicated and voluminous. For example, instead of merely reporting the displacement and rotation of the diaphragm, the output includes the displacements of all of the mesh nodes. This can be less burdensome if the software has the appropriate visualization and reporting tools. For example, RAM Structural System has a command that reports the deflection, drift, and drift ratio for any explicit location on the diaphragm selected by the user; the user needs to merely select the location, rather than digging through line after line of mesh node deflection values.
There is often some apprehension over the possibility of improperly meshing the diaphragm or assigning incorrect stiffness properties.
The question arises on the appropriate mesh size to use. What is the impact on the results if a coarse mesh is used versus a fine mesh?
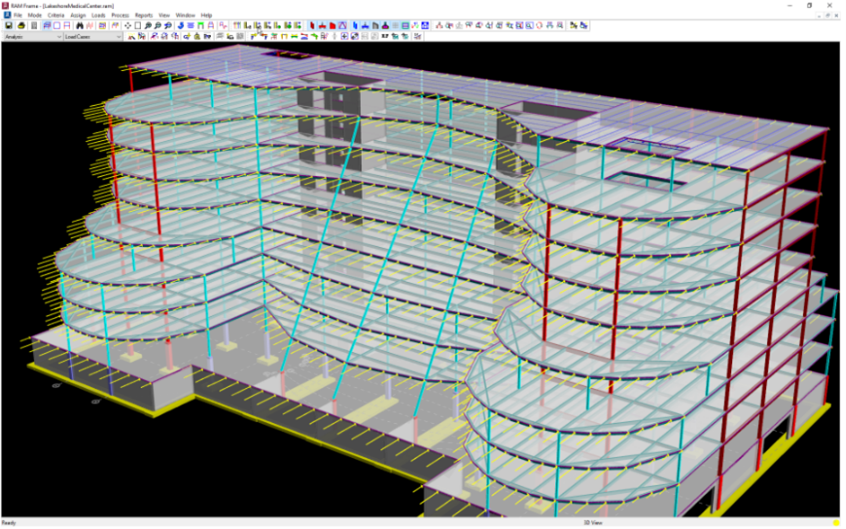
The structure shown here was analyzed in Bentley Systems’ RAM Structural System. This example structure was selected because of the asymmetry of the frames and the narrow diaphragms through the center of the floor plan.

The structure was analyzed several times with semirigid diaphragms, using a range of mesh sizes from 1 ft to 15 ft. The figure below shows a comparison of the 1-foot mesh versus the 15-foot mesh. For comparison, the model was also analyzed with the diaphragms specified as Rigid.

For each analysis the story shear at each level in each frame was tabulated. The table below shows the story shears (kips) at each story of each of the three transverse frames, for each mesh size.

Using the 1-foot mesh as a baseline, the values shown in parentheses are the percent difference between frame story shears for that mesh size and the 1-foot mesh size. As you can see, for this model, the story shears generally only varied by a fraction of a percent between the finest mesh and the coarsest mesh. The size of the mesh used in the analysis had very little impact on the distribution of the lateral forces; the analysis was not sensitive to the mesh size. It is important to note that the rigid diaphragm analysis didn’t compare well, with the frame story shears in error by over 50% in some cases. This is a good indication that some structures should not be analyzed using the rigid diaphragm assumption.
An important consideration is the impact of mesh size on the analysis time. For this structure the analysis took 2 seconds for the model with the 15-foot mesh, but it took 5 minutes 41 seconds for the model with the 1-foot mesh. For larger, more complicated structures it may be more practical to use a bit coarser mesh, to reduce the analysis times. From this exercise, we can see that a small refined mesh isn’t necessary, and that a reasonably large mesh gives acceptably accurate results with the benefit of substantially faster analysis times.
In addition to the frame story force comparison discussed above, the results for several other structural responses were similarly tabulated and compared. Space doesn’t allow for an exhaustive presentation of those results here, but a few things are noteworthy. The impact of mesh size on the diaphragm shear across the narrow segment of diaphragm was considerably more pronounced: there was a 22% difference between the value given with the 15-foot mesh and that given with the 1-foot mesh. That difference dropped to 5% for the 8-foot mesh and was 1% for the 4-foot mesh. The story drift at the most critical end of the structure also was impacted, but to a lesser extent: there was a 6% difference between the value given with the 15-foot mesh and that given with the 1-foot mesh. That difference dropped to 3% for the 8-foot mesh and was 2% for the 4-foot mesh.
For practical reasons I recommend specifying a larger mesh, say 4 ft or even 8 ft. The accuracy is within a small few percent or even a fraction of a percent of a more refined mesh, but the analysis times are dramatically shorter. You will work more productively.
You need to recognize that this is just one small example, and the study was certainly not exhaustive. You should take advantage of the analytical tools that are now available to you to create your own models and do your own studies. You need to decide for yourself what you are comfortable with.
Looking for more information? Fill in the form and we will contact Bentley for you.